One of the biggest challenges I’ve seen in organizations who want to work with graphs is the simplicity of a graph is often hidden beneath lengthy dissertations on what a graph can be, should be, would be if we handed it to a team of data scientists, etc. Graphs are essentially straightforward entities which can (and all too often do) have lots of cool names and features.
So let’s keep it simple, shall we?
What Is a Graph? What Can It Be Used For?
At the heart of every graph are two fundamental building blocks: nodes and edges. Nodes (sometimes called vertices) are the individual entities in your network—they could represent people, places, computers, or any distinct object. Edges are the connections between these nodes, representing relationships like “is friends with,” “is connected professionally,” or “is a road segment.” What makes graphs particularly powerful is that both nodes and edges can have attributes—additional pieces of information that provide context.
For instance, in a downtown street graph, an intersection node might have attributes like number of lanes, whether there is a light or stop sign, or lane restrictions, while a street edge might have an attribute indicating speed limit or the number of available lanes. Attributes enrich the graph such that we can start asking some very useful questions.
Let’s take a tangible example. Below you can see a simplified street map of a small town. We’ve got a Main Street, a few Avenues, and four cross-streets.
Now let’s turn this into a graph. This is an area where folks can often go astray. What would a node be? This is where graph thinking starts to become important. What we care about here is understanding connections (aka edges). Clearly we have streets doing the connecting. So what are they connecting to? Intersections. Ahh! So our nodes would be intersections, and our edges are the streets connecting them. With this in mind, we can now create a graph representation of our small downtown.
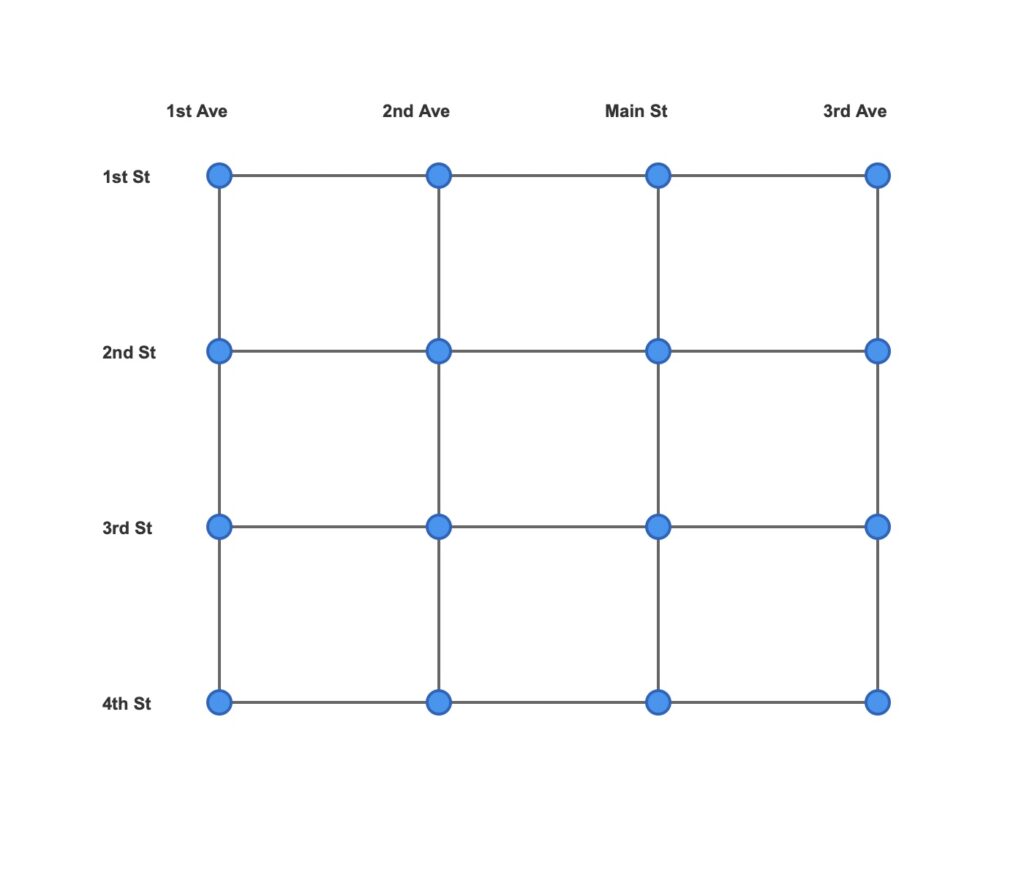
Now we can bring the power of graph to bear on our questions. Once I’ve added attributes such as street capacity, speed limit, lights, stop signs, merges, commute lanes and hours, etc. I’m ready for analysis. Here are a few simple things I could ask of this graph:
– What is the shortest path from the intersection of 1st Street & 1st Avenue to 4th Street & 3rd Avenue?
– How many different routes exist between 1st Street & Main Street and 3rd Street & 2nd Avenue that don’t backtrack?
– If the street segment between 2nd Street & 2nd Avenue and 2nd Street & Main Street is closed for construction, what’s the detour distance for vehicles traveling along 2nd Street?
While these are interesting questions, we haven’t really used the power of graph yet because they don’t take the reality of the roads into account. Given that the graph now reflects stop lights, stop signs, speed limits, number of lanes, etc., what more useful questions can I ask? Here are a few:
– What is the fastest route from 1st Street & 1st Avenue to 4th Street & 3rd Avenue, considering speed limits on each street segment and stoplight or stop sign delays at intersections?
– If I want to minimize total travel time from 3rd Street & 3rd Avenue to 1st Street & 1st Avenue, where some streets have school zones (15 mph) during certain hours and four-way stops always add 10 seconds each, what’s my optimal route?
Now we’re getting somewhere! But so far, we’ve been asking very specific questions of our graph by starting from a particular spot. There are often unknown patterns that we need to search for in a graph to uncover new insights. To find these requires a graph-wide search. Here are just a few questions we can ask to find the unknowns:
– If we close Main Street entirely for a parade, does the street network remain connected, or are some intersections completely cut off from others?
– Which intersection is the most “central” to the downtown network – meaning it has the minimum average drive time to all other intersections?
Now we see the real power of graph. It allows us to quickly identify the simple stuff (e.g. the shortest path from one spot to another), the more interesting stuff (e.g. the fastest path from one spot to another), and the very interesting stuff (do we break the town if we close Main street for a parade?). In this last example, I lived through what happens when you don’t do this analysis–in Boston, Massachusetts, during the notoriously messy “Big Dig”. Entire streets in Boston were accidentally rendered inaccessible by closures, which drove locals to do things like drive through construction parking lots to get where they were going. I did it myself more than once. While it sometimes worked, it was no bueno for the cab driver who was trying to find his way across the North End one evening and drove into a 30-foot deep hole!
So whether you’re a driver, first responder, urban planner, or business owner, this graph can help you be more effective at what you do. And creating the graph definitely was not rocket science!
Stay tuned for the next installment in this series: “A Node by Any Other Name” in which I will discuss and clarify common graph terms.




